美国海军惯性导航系统浅谈
在没有GPS定位系统的年代，确定战舰在海上的位置是一个比较棘手的问题。解决这个难题，不仅对于规划航线有着巨大的意义，对于战斗时的战场态势标绘同样意义非凡。一般来说，在那个年代，这个问题是通过惯性导航系统来解决的；而在惯性导航系统失灵时，也可以通过其他辅助设备，经由人工对战舰的航迹进行标绘。
1.陀螺罗经[编辑 | 编辑源代码]
几乎所有战舰的惯性导航系统都是基于同一原则设计的——如果出发地已知，给定出发时的方向和在该方向上航行的距离，就可以判断出终点和出发点的相对位置。如以出发点为原点，向北偏东30度方向航行3海里，则终点就在出发点的北偏东30度方向3海里处。因此，该系统必须要有准确的方向和距离的参数输入。
方向的输入是由陀螺罗经实现的。该装置是一种利用陀螺的定轴性、视运动以及进动性来自动找北的装置。
（1）陀螺的定轴性[编辑 | 编辑源代码]
根据角动量守恒定律，当高速旋转的刚体所受合外力矩为0时，刚体转动产生的角动量矢量保持不变。将该定律套到陀螺上，则不难得出，高速转动的陀螺在不受外力作用的情况下，其轴向始终保持某一固定方向——因为在陀螺中，角动量矢量的方向是同轴向重合的。
（2）陀螺的视运动[编辑 | 编辑源代码]
根据定轴性我们可以推知，若空间中有一个可以朝任意方向翻转的陀螺，当陀螺开始高速转动时，陀螺相对于空间的姿态应该是保持不变的。此时如果将该陀螺放置到地面上，则因为地球在自转，相对于空间静止的陀螺与地面之间就会产生相对运动。具体来说，如果一个可以自由翻转且正在高速自旋的陀螺沿南北向被放置在北半球，则陀螺轴的指北端会向东旋转，指南端会向西旋转；反之，如果该陀螺被沿南北向放置在南半球，则陀螺的指北端会向西转，指南端会向东转。倘若该陀螺是沿东西向放置的，则不论该陀螺处于北半球还是南半球，其指东端都会相对于地面升高，指西端则会相对于地面降低。由于该运动并非陀螺相对于空间的运动，而是陀螺相对于地面及地面上的观察者的视觉运动，因此被称为陀螺的视运动。
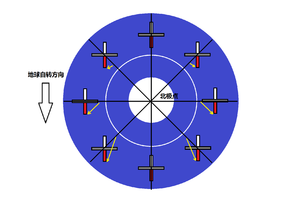
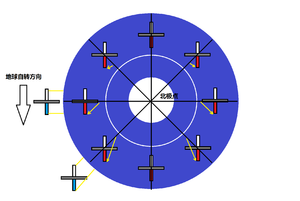
（3）陀螺的进动性[编辑 | 编辑源代码]
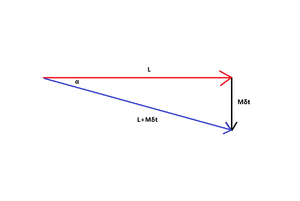
进动性是陀螺在受到不为零的外力矩作用时表现出的运动性质，该性质可通过外力矩引起的角动量变化解释。如图所示，有一个初始角动量L，一个外力矩M作用在该角动量的矢端。根据公式δL=Mδt，可知在一个极短的时间δt内，外力矩M将会引起一个垂直于初始角动量、模长=Mδt的角动量增量。根据矢量相加的三角形法则，合成后的新角动量应该由初始角动量的尾端指向角动量增量的矢端；因为角动量增量不为零，新角动量与初始角动量之间就会产生一个偏角α。从宏观上来看，就是当高速旋转的陀螺受到外力作用时，将会沿着同时垂直于轴向和外力作用方向的第三个方向偏转，并且转动方向同陀螺自旋方向有关。
（4）进动方向的右手螺旋定则[编辑 | 编辑源代码]
考虑到不是什么时候都有条件画矢量叠加图的，这里提供一种能够快速判断陀螺进动方向的方法：
首先伸出右手，令大拇指与其余四指垂直，再令其余四指沿着陀螺的自转方向弯曲，记下此时大拇指的指向（角动量方向）；再摊开右手，保持四指与大拇指垂直的关系不变，令四指由陀螺轴的支点指向外力的作用点，再调整掌心的方向使掌心正对外力的正方向，抓起四指使四指指尖指向外力正方向，记下此时大拇指的方向（外力矩方向）。想象一下有一个力作用在第一次确定的大拇指的头上，并沿第二次确定的方向拉动大拇指，该拉动方向就是陀螺的进动方向。如第一次确定的方向是水平向左，第二次确定的方向是垂直向下，则进动方向就是外力矩垂直向下拉动水平向左的角动量的矢端，也就是逆时针方向。
（5）斯佩里式陀螺罗经[编辑 | 编辑源代码]
此处以斯佩里式陀螺罗经为例。
当一个水平放置的陀螺下方悬挂了一个装满高密度液体的连通器时，就制成了一个不完全的斯佩里式陀螺罗经。倘若该陀螺的轴沿东西方向放置，且陀螺自下而上旋转，则根据陀螺的视运动规律，右侧的指东端会向上升起，而左侧的指西端则会下降；由于连通器两端出现高度差，连通器内的液体将会由较高的右侧向较低的左侧流动，使左侧重力大于右侧重力，在陀螺左侧产生一个向下的重力偏转力；根据陀螺的进动规律不难得出，此时陀螺会逆时针进动，即陀螺轴靠向南北方向。但由于此时陀螺依然受视运动规律支配，尚未转到正北方向的右侧指东端还会继续升起，直至陀螺轴完全转至南北方向时达到最高点；在此过程中，由于连通器的斜度越来越大，重力偏转力也越来越大，最后导致陀螺以很快的速度越过南北方向，继续沿逆时针方向旋转。考虑到指东端越过南北方向后就变成了指西端，原先的指东端又会慢慢下降，直至陀螺轴回到东西方向后恢复水平。
但是，因为陀螺转过180度后，从正面观察，原先自下而上的旋转方向会变成自上而下，此时陀螺的角动量方向将会发生镜面翻转，变成指向右侧。而由于陀螺的视运动规律，陀螺指向右侧的一端又会向上升起，左侧再次下降，重新产生一个方向相同——垂直纸面向外——的外力矩。外力矩垂直向外拉动指向右上的大拇指的头，就会造成大拇指向顺时针方向旋转，即陀螺开始产生沿顺时针方向反向进动的趋势。在该趋势下，陀螺轴沿逆时针方向的运动会逐渐减速直至停止，随后又开始沿顺时针方向加速进动，直至陀螺轴再一次镜面翻转。于是，陀螺轴便在南北方向的两侧不断来回翻转。此时如果再给陀螺安装一个阻尼装置，使有规律的、以南北方向为对称轴的顺逆时针摆动逐渐收敛，最终稳定在南北方向不变，就能使陀螺轴稳定指北，斯佩里式陀螺罗经就诞生了。
2.水压式航速计[编辑 | 编辑源代码]
水压式航速计的作用是测定单位时间内战舰相对于海水的位移，即战舰的航速。如果单位时间内战舰相对于海水的位移已知，时间已知，就可以推出战舰在该时间内走过的航程。
水压式航速计的原理较陀螺罗经更为简单。简而言之，它利用的是伯努利原理，即流体压强和流速的关系。
（1）伯努利原理（伯努利方程）[编辑 | 编辑源代码]
对于理想液体，有：
ρgh+P静+（ρv²）/2=P总
其中P静+（ρv²）/2称为全压，ρ是当地流体密度。不难看出，如果可以测出流体的全压和静压，就可以根据全压-静压=（ρv²）/2推出流体流速v。完成这一过程的装置叫皮托管。
（2）皮托管[编辑 | 编辑源代码]
皮托管的构造是一根“套管”。其中外管是根头部封闭的盲管，前部的外壁上开有若干测量孔，而内管的管口则开在外管的头封上，是一根通管。内外管的尾端分别都接有压力传感器。当皮托管在水中运动时，前方来流通过内管在头封上的开口冲进内管里，并冲击内管尾端的压力传感器，输出流体全压P1；而内外管之间则是近似的静水，所以接在外管尾部的压力传感器测得的是流体的静压P2。此时根据公式，有流体动压=全压-静压=P1-P2=ρv²/2，变形后有v²=2（P1-P2）/ρ，流速v=根号下【2（P1-P2）/ρ】。
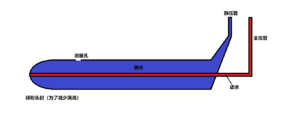
3.DRT与FRAI[编辑 | 编辑源代码]
DRAI[编辑 | 编辑源代码]
DRAI，全称为Dead Reckoning Analyzer Indicater，即航位推算分析指示器，是一种用于处理输入的航向信息和航速信息的机械式计算机。经过该装置的处理后，沿某一方向的速度会被分解为水平和垂直方向的各一个分量，并分别输出进入后面的DRT。
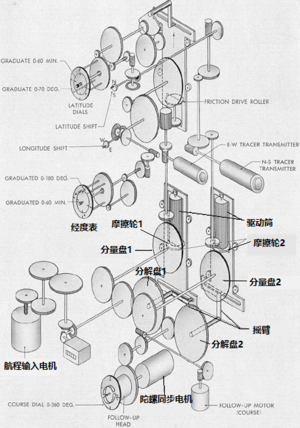
典型的DRAI内部结构如图所示。装置的核心是两个完全一样的变速器：变速器有一个倒T形的外框，外框内沿纵向装有一个直径均匀的驱动筒。驱动筒的下端装有一个摩擦轮。用于输出信号的输出轮压在驱动筒的表面，可沿驱动筒的轴向自由滑动。两个变速器的摩擦轮都压在一个完全相同的分量盘上；分量盘由同一个齿轮带动，而该齿轮则由一个航程输入电机驱动。航程输入电机与来自皮托管航速计的航速信息同步，其单位时间内旋转的圈数同测得的航速成正比例关系。另外有一个陀螺同步电机，该电机的旋转与陀螺罗经的偏转同步；陀螺同步电机通过齿轮带动一左一右两个分解盘，用于对输入的航向信息进行正交分解。两根摇臂分别和两个分解盘同轴相连，相互呈一个90度的夹角；且摇臂的长度均等于分解盘和分量盘的半径R，摇臂的另一端则卡在变速器倒T型框架底部的滑槽里。当摇臂旋转时，由于摇臂在水平方向上可以独立于变速器框架自由滑动，框架不会由摇臂带动产生水平方向的位移，只会产生垂直方向的运动。
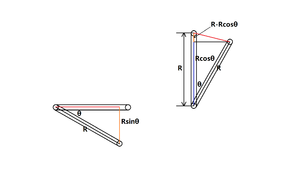
现假设陀螺同步电机产生了一个角度为θ的偏转。那么不难看出，左侧摇臂头在垂直方向上的位移是Rsinθ，而右侧摇臂头的位移则是R-Rcosθ。受摇臂驱动，两个框架连同上面的摩擦轮也分别在垂直方向上移动了Rsinθ和R-Rcosθ。由于左侧的摩擦轮初始位置在左侧分量盘的中心，而右侧摩擦轮的初始位置则在右侧分量盘的上缘，移动后两个摩擦轮距离分量盘中心的距离分别是Rsinθ和R-（R-Rcosθ）=Rcosθ；由线速度公式ωR得，左右摩擦轮的转速分别为ωRsinθ和ωRcosθ，即经由驱动筒到输出轮输出的转速之比为sinθ：cosθ。所以，左边的变速器就输出了航速的正弦值，即航速沿东西方向的分量；而右边的变速器输出的则是航速的余弦值，即航速沿南北方向的分量。随着时间的推移，就可以分别得到战舰沿东西方向和南北方向的位移。
DRT[编辑 | 编辑源代码]
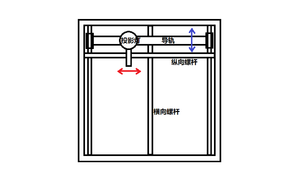
全名为Dead Reckoning Tracer的DRT是导航系统的显示终端。该装置接收来自DRAI的两个航速信息，并将这两个航速重新合成为速度矢量，随时间的推移绘制出战舰在该方向上的位移。装置内部包括一纵一横两根螺杆；其中横向螺杆接收东西方向的速度分量，可以推动纵向螺杆左右移动，而纵向螺杆则接收南北方向的速度分量，可以带动其上的投影灯前后移动。由此，原先由DRAI正交分解的速度矢量在DRT内又被重新以正交的方式合成，推动玻璃台面下的投影灯随时间移动。由于投影灯的光亮很强，足够透过固定在DRT玻璃台面上的海图，操作人员可以很清晰地看到一个在海图上移动的亮斑。每隔一分钟，操作人员都会在亮斑的中心用铅笔标出一个点，代表该时刻战舰的位置；把这些标出的点连起来，就能得到战舰在过去一段时间内的连续航迹。
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||